In Part 1 and Part 2, we showed some properties of a classic pseudo-random number generator, the linear congruential generator. In this part, we will introduce a more recent generator, splitmix64. Splitmix64 was created in 2013 as part of Java 8.
Splitmix64
Splitmix64 (called SplittableRandom1 in Java 8) use the following operations over 64-bit unsigned integers: addition, multiplication, exclusive or, and bit shifting. Below is a simple version in Julia:
function build_splitmix64(seed::UInt64)
state = seed
function sliptmix64()
state += 0x9e3779b97f4a7c15
z = xor(state, state >> 30) * 0xbf58476d1ce4e5b9
z = xor(z, z >> 27) * 0x94d049bb133111eb
xor(z, z >> 31)
end
endbuild_splitmix64 (generic function with 1 method)
A quick quality check
Let’s take a seed equal to 0x1234567890123456:
seed = 0x1234567890123456
splitmix64 = build_splitmix64(seed)(::getfield(Main, Symbol("#sliptmix64#3"))) (generic function with 1 method)
We plot below the bits of the first 16384 generated numbers. Since \(16384 \times 64 = 1024 \times 1024\), we plot a \(1024 \times 1024\) matrix.
using PyPlotbits = zeros(Bool, 1024, 1024)
number = 0
for i in 1:1024
for j in 1:1024
if j % 64 == 1
number = splitmix64()
end
bits[i, j] = number & 1
number >>= 1
end
end
imshow(bits)
title("2^14 numbers generated by splitmix64")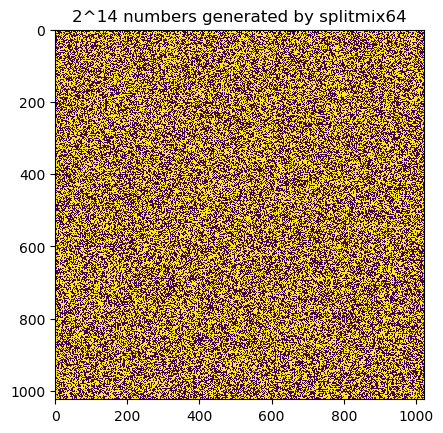
PyObject Text(0.5, 1.0, '2^14 numbers generated by splitmix64')
We don’t notice any specific pattern on the above plot of the first \(2^{14}\) generated numbers, that’s good. Let’s write a simple test function that a LCG would fail. We will just count the total number of ones for each 64 bits of a subsequence of generated numbers.
function check_subseq(delta, repeat=100, iter=2^16)
count = zeros(Int, repeat, 64)
x1 = splitmix64()
x = 0
total = 0
for r in 1:repeat
for i in 1:iter
x = splitmix64()
if i % delta == 0
total += 1
for j in 1:64
count[r, j] += (x - x1) & 1
x >>= 1
end
end
end
end
count, div(total, repeat)
endcheck_subseq (generic function with 3 methods)
Let’s try on the subsequence \(\left(x_{32i}\right)_{i}\):
using Statisticscount, total = check_subseq(32)
println("total generated numbers: ", total)
println("mean: ", mean(count))
println("std: ", std(count))
println("median: ", median(count))
println("min: ", minimum(count))
println("max: ", maximum(count))total generated numbers: 2048
mean: 1024.23453125
std: 22.539163771426786
median: 1024.0
min: 945
max: 1107
These values don’t seem bad. Indeed, for 2048 truly random numbers, the probability of each bit being 1 is 0.5 and therefore the expected value of the count is 1024.
We will not go further in the analysis of this pseudo-random number generator. Splitmix64 has been reported to pass the tests of the testing suite Dieharder. Probably only a very deep analysis might reveal anomalies.
Reversing Splitmix64
We will show in this section that we can easily get the value of the internal state from the value of the ouput.
First, notice that splitmix64 uses three times the following operations: taking the exclusive or of a value and a bitshift of this same value. This operation is easy to reverse.
For example, let’s consider that we do a rightshift of 31 bits to a value \(x\) and xor it with \(x\). \(x \gg 31\) left 31 bits are equal to 0 and therefore the left 31 bits of \(y = x \oplus (x \gg 31)\) are the left 31 bits of \(x\). But knowing the left 31 bits of \(x\) means that we know the left 62 bits of \(x \gg 31\). Since we also know the value of \(y\), we can deduce the value of the left 62 bits of \(x\). Knowing these 62 bits means that we know all the bits of \(x \gg 31\) and we therefore can get all the bits of \(x\).
Below is a simple Julia function to reverse the operation \(x \oplus(x \gg shift)\):
function reverse_xorshift(y, shift)
delta = 64 - shift
x = y >> delta << delta
reversed = shift
delta -= shift
while reversed < 64
x += xor(y << reversed >> reversed, x << (reversed - shift) >> reversed) >> delta << delta
delta -= shift
reversed += shift
end
x
end reverse_xorshift (generic function with 1 method)
The next operation to reverse is the integer multiplication modulo \(2^{64}\). Odd numbers can be inversed thanks to a Newton’s method2. Below is the code:
function reverse_odd_number(x)
@assert isodd(x)
r = x
for _ in 1:5
r *= 2 - r * x
end
r
endreverse_odd_number (generic function with 1 method)
We now just have to use the two previous functions to reverse the whole splitmix64 and get back the internal state:
splitmix64 = build_splitmix64(seed)
y = splitmix64()
x = reverse_xorshift(y, 31)
x *= reverse_odd_number(0x94d049bb133111eb)
x = reverse_xorshift(x, 27)
x *= reverse_odd_number(0xbf58476d1ce4e5b9)
x = reverse_xorshift(x, 30)
x -= 0x9e3779b97f4a7c15
print("Reversing splitmix64, we get the value: ")
show(x)
print("\nWe now check if this is equal to the original seed: $(x == seed)")Reversing splitmix64, we get the value: 0x1234567890123456
We now check if this is equal to the original seed: true
We see that knowing the value of the output actually gives us the value of the internal state. We can therefore predict all the future generated numbers.
A pseudo-random number generator may have good statistical properties and yet be very easy to reverse knowing only a few values of the output. If being able to easily guess the future values from a sample of past values is a problem for your application, you should consider using a cryptographically secure pseudo-random number generator (CSPRNG).
Notes:
[1] SplittableRandom source is available at hg.openjdk.java.net/jdk8/jdk8/jdk/file/tip/src/share/classes/java/util/SplittableRandom.java
[2] a detailed explanation of computing the inverse of an odd number is available at lemire.me/blog/2017/09/18/computing-the-inverse-of-odd-integers/