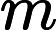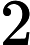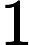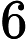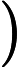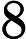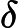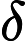We introduced in Part 1 the linear congruential generators. In this second part, we will show some defects of such generators, considering the case where the modulus is a power of 2.

Testing a LCG with modulus \(m = 2^{16}\)

Keeping the notations from Part 1, we saw that \(m\) being the number of possible internal states, the sequence has to repeat itself partly or fully before or when \(m+1\) numbers are generated. The Hull-Dobell theorem tells us how to choose the parameters of a LCG to get a period of maximal length.
We will test some very simple properties that we would expect from a good uniform pseudo-random number generator.

Let’s use again the function defined in Part 1:

function build_lcg(m, a, b, seed)
    f = x -> a * x + b
    state = seed
    function get_next_number()
        state = f(state) % m
    end
end
build_lcg (generic function with 1 method)

We create a LCG with the following parameters:

m = 2^16
a = 4 * 4321 + 1
b = 8671
seed = 5423
get_next_number = build_lcg(m, a, b, seed)
get_next_number (generic function with 1 method)

We know from the Hull-Dobell theorem that, with the above chosen parameters, the period is maximal and each number will appear exactly once during each period. This is already a first nice property if we want to use the sequence of generated numbers for shuffling. Let’s try now to apply some tests to the generated numbers.

Rather than working on the whole output range that can be huge, we can do some tests at the bit level. If a number is “random”, its bits should also be “random”. When the output range is of the type \(0 \dots 2^{n}-1\), i.e. \(m = 2^{n}\), each one of the \(n\) bits should appear with an equal probability \(1 / n\) whatever subsequence of the generated sequence we consider.

Let’s first plot all the bits of the \(2^{16}\) 16-bit numbers generated during one period of our function. This means that we will plot \(2^{16} \times 16 = 2^{20} = 1024 \times 1024\) bit values. We therefore create a \(1024 \times 1024\) matrix. The first row of the matrix will contain the bits of the first 64 generated pseudo-random numbers, the second row the bits of the next 64 generated numbers (i.e. the bits of the 65th to 128th number), …

using PyPlot
bits = zeros(Bool, 1024, 1024)
number = 0
for i in 1:1024
    for j in 1:1024
        if j % 16 == 1
            number = get_next_number()
        end
        bits[i, j] = number & 1
        number >>= 1
    end
end
imshow(bits)

png

PyObject <matplotlib.image.AxesImage object at 0x7fa3f19daf28>

We can see many vertical lines, this doesn’t look random at all1. It means that we can easily find a subsequence with at least one bit that stays constant. For example, if we take only every other generated number, we get numbers with the same parity!
This a common property of all the linear congruential generators of maximal period with \(m\) being a multiple of 4. Indeed, let \(x_{i}\) be one of the generated numbers. The next number \(x_{i+1}\) will be equal to \(ax_{i} + b \pmod m\) and the following one, \(x_{i+2}\), to \(a (ax_{i}+b) + b \pmod m\). Therefore we have: \[ \begin{equation} \begin{split} x_{i+2} - x_{i} &= a (ax_{i}+b) + b \pmod m\\ &= x_{i} (a^2 - 1) + b (a + 1) \pmod m. \end{split} \end{equation} \] Since \(m\) is a multiple of 4 and the generator has a period of maximal length, we know that there is a \(k>0\) such that \(a = 4k + 1\). Consequently, \[x_{i+2} - x_{i} = x_{i} \left((4k+1)^2 - 1\right) + b \left(4k + 2\right) = 2 \left( x_{i} (8k^2 + 4k) + b (2k + 1) \right)\pmod m\] and \(x_{i+2}\) and \(x_i\) have same parity.

Actually, this property is even more general: every subsequence \(\left(x_{\delta i + c}\right)_{i}\) with \(\delta = 2^p\) and \(c \le \delta\) has identical last \(p\) bits. Let’s just write a simple function to check this result:

function check_subseq_modulo(delta)
    x1 = get_next_number()
    x = 0
    for i in 1:2^16-1
        x = get_next_number()
        if (i % delta == 0) && ((x - x1) % delta != 0)
            println("The first generated number and $(i+1)-th number have different values modulo $(delta): $(x % delta) and $(x1 % delta).")
            return false
        end
    end
    println("The subsequence (x_$(delta)i) is constant modulo $(delta), with value $(x1 % delta)")
end
check_subseq_modulo (generic function with 1 method)

check_subseq_modulo(512)
The subsequence (x_512i) is constant modulo 512, with value 74

Let’s come back to our previous plot. There were 64 generated numbers per row. That means that if we look only at the first 16 columns, we get a subsequence with \(\delta = 64 = 2^6\). Below is a plot of the subsequences \(x_{\delta i + c}\) for \(c \in 1 \dots 4\) and \(i \in 0 \dots 63\):

for c in 1:4
    subplot(1, 4, c)
    imshow(bits[1:64, (c-1)*16+1:c*16])
    title("c = $c")
end

png

We see that indeed the first six bits of each sequence stay constant. Therefore the generated bits are far from being “random”.

Different uniform random number generators testing suites are available, for example Dieharder, TestU01 or Practically Random. Failing one or more tests of a suite means that the “random” number generator has some non-random properties. However, passing all the tests doesn’t mean that the random generator is perfect, it just means it is good with respect to a big amount of tests. As it is expected, LCGs fail some tests of these suites.

In Part 3, we will introduce a more recent generator, splitmix64.



Notes:
[1] a similar plot can be found at www.random.org/analysis/#visual as well as a comparison to their hardware random number generator.

Reference:
Knuth, The Art of Computer Programming, Volume 2, Chapter 3